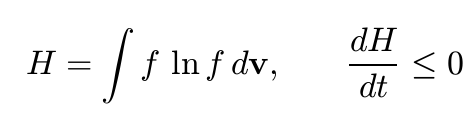Significato matematico della quantità H e introduzione del calcolo delle probabilità
Nelle “Lezioni sulla Teoria dei Gas” di Boltzmann del 1898, tradotte da Rossani e a cura di Badino, possiamo trovare un importante lavoro su di un gas con volume unitario.
L’autore inizia parlando dei principi del calcolo delle probabilità, prendendo ad esempio un’urna contenente molte sfere nere e in ugual numero bianche e proponendo di fare 20 estrazioni puramente casuali, con reinserimento. La probabilità di estrarle tutte nere è la stessa di altre possibili estrazioni e il fatto che sia più probabile estrarne 10 bianche e 10 nere piuttosto che tutte nere dipende dal fatto che l’evento 10-10 può avvenire in molti più modi dell’evento 20-0. Se rapportiamo le due probabilità abbiamo 20!/(10!10!) che indica quante permutazioni possiamo fare dei termini della serie di 10 bianche e 10 nere, trattando le differenti sfere bianche e nere come identiche. Se aumentiamo i colori abbiamo la probabilità di estrarre “a” sfere di un certo colore, “b” di un altro, ecc. pari ad un numero (a+b+c+…)!/(a!b!c!…) di volte più grande di estrarre sfere di un solo colore. Ebbene:
l’evento che tutte le molecole in un gas abbiano esattamente la stessa velocità e direzione di moto non è affatto meno probabile dell’evento che ciascuna molecola abbia esattamente la velocità e direzione di moto che effettivamente ha in un particolare istante nel gas. Ma se confrontiamo il primo evento con l’evento che la distribuzione maxwelliana di velocità vale nel gas, troviamo che a quest’ultimo appartengono molte più configurazioni equiprobabili.
E poi Boltzmann procede a legare questa legge con il funzionale H del teorema omonimo, utilizzando la formula di approssimazione al continuo “p! = radice(2 pigreco p)(p/e)^p” con “e” base dei logaritmi naturali, dividendo lo spazio in cellette di volume omega e introducendo la funzione “Z” equivalente al numero calcolato prima (in grassetto). A questo punto l’autore afferma:
Il teorema […] che afferma che H decresce a causa delle collisioni, dice semplicemente che, per via delle collisioni, la distribuzione di velocità delle molecole del gas si avvicina progressivamente a quella più probabile, considerando lo stato molecolarmente disordinato, e in questo modo si introduce il calcolo delle probabilità.
E continua rispondendo alle questioni sulla reversibilità e, in sostanza, alla validità delle ipotesi di disordine molecolare che garantiscono la validità del teorema H.
Infine riflette sul numero grande ma comunque finito delle molecole per unità di volume e sui fenomeni le cui proprietà del gas non sono grandi rispetto al libero cammino medio, per poi dire:
Tutti gli altri fenomeni hanno luogo in spazi così grandi che si può costruire un elemento di volume per cui il moto visibile del gas può essere preso come differenziale che contiene ancora un grande numero di molecole. […] La legge di distribuzione delle velocità molecolari non è precisamente corretta, non essendo il numero di molecole matematicamente infinito. Lo svantaggio di abbandonare la supposta validità esatta delle equazioni differenziali idrodinamiche è tuttavia compensata da una maggiore chiarezza.
Possiamo dunque osservare con quale destrezza Boltzmann introduce argomenti statistici all’interno della meccanica, mantenendo da un lato una visione d’insieme e dall’altro lato un’estrema attenzione ai dettagli matematici.
Considerazione sulla legge matematica (a+b+c+…)!/(a!b!c!…). Siamo di fronte ad una applicazione della formula di Bernoulli (presumo Jakob, 1654-1705): si veda il video #qui per una trattazione didattica.