Liberto - Il principio di entropia

Corrente di entropia, conduzione termica e ambiguità sulla potenza dissipata

28 Agosto 201531 Agosto 2015

Ho trovato #qui un lavoro del liceo cantonale di Locarno (D’Anna) ove si parla di conduzione termica utilizzando i concetti di “corrente di energia” e di “corrente di entropia” per indicare il flusso di energia e di entropia nell’unità di tempo, tra due sistemi che interagiscono termicamente. Il rapporto tra essi è proprio la temperatura assoluta alla quale avviene lo scambio, per cui abbiamo $I_{E} = T\cdot I_{S}$ .

Si parla inizialmente della legge di Fourier costruendola in questo modo: la differenza di temperatura ai capi del conduttore è proporzionale alla corrente di energia, in base alla “resistenza termica” $R_{term} = \bigtriangleup T / I_{E}$ la quale è direttamente proporzionale alla lunghezza del conduttore e inversamente proporzionale alla conducibilità termica e alla sezione del conduttore.

Poi ci si sofferma alla situazione di stato stazionario per cui la corrente di energia entrante è uguale a quella uscente. Tuttavia le correnti di entropia sono differenti, in quanto l’interazione termica tra conduttore e ambiente avviene a temperature differenti (l’ambiente è suddiviso infatti in due sistemi non interagenti i quali mantengono la loro temperatura costante nel tempo). Nello specifico se abbiamo $T_{1}> T_{2}$ allora vale $I_{S_{1}}< I_{S_{2}}$ il cui significato è questo: durante la propagazione dell’energia attraverso il conduttore viene prodotta entropia e questa è la dimostrazione che la conduzione termica è un processo irreversibile.

Una prima domanda interessante è la seguente: dove viene prodotta l’entropia? Il tasso di produzione di entropia è la somma di tutti i contributi in ogni tratto spaziale del conduttore ed è dato da $\pi_{S}=I_{S_{2}}- I_{S_{1}}$ ; vale infatti l’additività della produzione di entropia.

Una seconda domanda invece mi ha messo molto in discussione: a quale temperatura viene prodotta entropia? L’autore risponde con $T_{2}$ proponendo la seguente ottima immagine riassuntiva che indica anche, secondo definizioni precedenti, la potenza termica $P_{term}=I_{S}} \cdot \bigtriangleup T$ e la potenza dissipata $P_{diss}=\pi_{S} \cdot T$

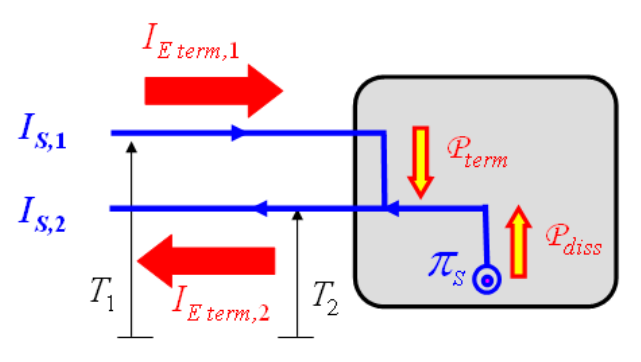Il problema però dei seguenti passaggi algebrici 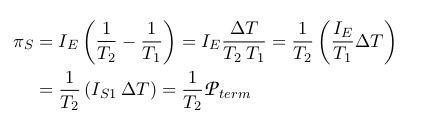è che nel terzo passaggio viene scelto senza giustificare di raccogliere $T_{2}$ , quando si potrebbe raccogliere l’altra temperatura. Questo significa che si possono avere diverse potenze dissipate, ad esempio $\pi_{S} \cdot T_{2}$ oppure $\pi_{S} \cdot T_{1}$ . Ho trovato ad esempio #qui (Liberto) un articolo che preferisce la seconda delle due formule appena citate. Come mai? Se si considera la potenza dissipata come il lavoro che avremmo potuto eseguire con una macchina termica reversibile, abbiamo due situazioni: o prendiamo calore $Q$ da $T_{1}$ e cediamo $Q \cdot T_{2}/T_{1}$ a $T_{2}$ , o prendiamo $Q \cdot T_{1}/T_{2}$ da $T_{1}$ e cediamo $Q$ a $T_{2}$ . Nel primo caso abbiamo la prima potenza dissipata, nel secondo caso la seconda (i calcoli sono semplici). Ebbene, siccome il calore $Q$ nell’unità di tempo – cioè la corrente di energia – è uguale in entrata e in uscita, l’unico elemento di preferenza è la quantità di potenza dissipata. Allora è possibile preferire la maggiore dissipazione e quindi rispondere che l’entropia in un certo tratto di conduttore (all’interno del quale avviene conduzione termica) viene prodotta alla temperatura maggiore tra le due che si trovano ai capi del tratto stesso.